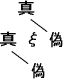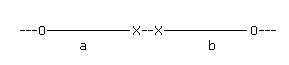- 4.001
- 命題の全体が言語である。
- 4.002
- 人は、それぞれの語が何をどのように意味しているか気づいていなくとも、あらゆる意義を表現することばを構成する能力をもっている。−−ちょうど、それぞれの音がどのように発せられるかを知らなくとも喋ることができるように。
日常言語は、人という有機体の一部であり、それに劣らず複雑である。
日常言語から言語の論理を直接取り出すことは人には不可能である。
言語は思考を偽装する。すなわち、衣装をまとった外形から、内にある思考の形を推測することはできない。なぜなら、衣装の外形は、体の形を示すこととはまったく違った目的でデザインされているのだから。
日常言語を理解するための暗黙の取り決めは途方もなく複雑である。
- 4.003
- 哲学的なことがらについて書かれたほとんどの命題や問いは誤っているのではなく、ナンセンスなのである。それゆえ、この種の問いに答えることは不可能であり、われわれはただそれがナンセンスであると確かめることしかできない。哲学者たちの問いと命題のほとんどは、われわれが自分の言語の論理を理解していないことから発生している。
(それらは、「善は美よりもより多く同一的であるのか、それとも、より少なく同一であるのか」といった問いと同類である。)
こうしてもっとも深遠な問題が実はまったく問題ではなかったとしても驚くべきではない。
- 4.0031
- すべての哲学は「言語批判」である。(もちろんマウトナーの言う意味においてではない。)ラッセルの功績は、命題の見せかけ上の論理形式が必ずしもその実際の論理形式である必要はないことを示した点にある。)
- 4.01
- 命題は現実の像である。
命題は、われわれが思い描く現実のモデルである。
- 4.011
- 一見したところ命題は−−たとえば紙に印刷されている場合−−、それが表している現実の像のようには見えない。しかし、楽譜もまた見たところ音楽の像のようには見えず、われわれの表音文字(アルファベット)も会話の像になっているようには思われないのである。
それでもこれら記号言語は、それが表すものに対して、普通の意味でも像となっている。
- 4.012
- 明らかにわれわれは「
aRb
」という形式の命題を像として受け止めている。ここにおいて記号は明らかにそれが表すものの似姿である。
- 4.013
- そこで像であることの本質へと踏み込むならば、そのときわれわれは、記号の外見上の不規則さ(楽譜における♯や♭の使用のような)は、それが像であることを妨げないことを見てとるだろう。
なぜなら、これら不規則なものもまた、単に異なる仕方で、その表現しようとすることを写像しているのだから。
- 4.014
- レコード盤、音楽的思考、楽譜、音波、これらはすべて互いに、言語と世界の間に成立している関係と同様に写像関係にある。
それらすべての論理的構造は共通である。
(童話の二人の若者、その二頭の馬、そして彼らの百合のように。それらはある意味ではすべて一つなのである。)
- 4.0141
- ある一般的な規則が存在し、それによって音楽家は総譜から交響曲を読みとることが可能となり、そしてそれによってレコード盤の溝から交響曲を引き出すことが可能となる。そして、最初の規則によって、交響曲から再び総譜を導き出すことができる。まさにこの点に、一見まったく相異なる形象の内的な類似性が横たわっている。そしてその規則とは、交響曲を音符言語に射影する射影法則であり、それは音符言語をレコード盤の言語に翻訳する翻訳規則である。
- 4.015
- われわれの表現方法のすべての像、すべての似姿は、写像の論理によって可能となっている。
- 4.016
- 命題の本質を理解するために、象形文字を考えるべきである、それは記述する事実を写像している。
そして象形文字がアルファベットになったときにも、その写像の本質は失われてはいないのである。
- 4.02
- われわれは、命題記号を説明されなくても、その意義を理解することができる。このことから、命題記号が象形文字と本質的に同じであることが分かる。
- 4.021
- 命題は現実の像である。−−なぜなら、命題を理解すれば、その命題が描写している状況を知るのだから。そして命題を理解するのに、その意義の説明を必要としないのだから。
- 4.022
- 命題はその意義を示す。
命題は、それが真ならば、事実がどのようであるかを示す。そして事実がそうであることを語る。
- 4.023
- 命題は、あとはイエスかノーかというところまで、現実を限定しなければならない。
そのためには、現実は命題によって完全に記述されねばならない。
命題とは事態の記述である。
対象の記述がその対象の外的性質によって記述されるように、命題は現実がもつ内的な性質によって現実を記述する。
命題は、論理的足場を頼りに世界を構築する。それゆえ、その命題が真であるならば、そこから論理的に何が言えるのかすべて見てとることができる。人は誤った命題からも推論することができる。
- 4.024
- 命題を理解するとは、それが真であるとすれば成立することはなにかを知ることである。
(それゆえひとは、実際に真かどうかを知らなくとも、命題を理解することができる。)
その構成要素が理解されれば、命題は理解される。
- 4.025
- ある言語から他の言語への翻訳は、一方の各命題から他方への命題へ翻訳されるのではなく、ただ命題の構成要素だけが翻訳される。
(そして辞書は名詞だけでなく、動詞、形容詞、接続詞等々の翻訳も行い、しかもそれらすべてを同等に扱う。)
- 4.026
- 単純記号(語)の意味を理解するには説明してもらわねばならない。
しかし、命題はおのずから理解される。
- 4.027
- 命題はわれわれに新しい意義を伝えることができる、これは命題の本質に属している。
- 4.03
- 命題は古い表現で新しい意義を伝えなければならない。
命題はわれわれにある状況を伝える。それゆえ、命題はその状況と本質的に結びついていなければならない。
そしてその結合とは、命題が状況の論理像であること、そのことである。
命題は、ただ像であるかぎりにおいてのみ、何ごとかを語る。
- 4.031
- 命題において状況はいわば実験的に構成される。
「この命題はしかじかの意義をもつ」と言う代わりに、単に「この命題はしかじかの状況を描写する」と言うことができる。
- 4.0311
- ある名はあるものを代表し、他の名はまた別のものを代表する、そしてそれらの名が互いに結合されている。そしてその全体が−−活人画のように−−事態を表現する。
- 4.0312
- 命題の可能性は記号が対象の代理をするという原理に基づいている。
しかし「論理定項」はなにかを代理しているのではない。すなわち事実の論理は記号で表すことができない。これが私の基本的考えである。
- 4.032
- 命題は論理的に分節化されているかぎりにおいてのみ、状況の像である。
(’Ambulo'[私は歩く]という命題も、やはり合成されたものである。なぜなら、その語幹に異なる語尾をつけても、その語尾に異なる語幹をつけても、意義が変わるのだから。)
- 4.04
- 命題は、それが描写している状況と正確に同じだけの部分に区分されなければならない。
命題と状況は、同じだけの論理的(数学的)多様性を持たねばならない。(力学上のモデルに関する、ヘルツの「力学」参照。)
- 4.041
- 言うまでもなく、この数学的多様性それ自身を再び写像することはできない。
それを写像しようとして、その外に出ることができないからである。
- 4.0411
- われわれが「
(x) . fx
」と表しているものを、仮に「fx
」の前に(一般性を示す)目印をつけて、たとえば「Alg.fx
」と表したとしよう。これでは十分ではない。−−これでは、なにが一般化されているのか分からない。そこでx
に一般性の目印 「a
」 を添えて「f(xa)
」のように表したとする。これもやはり十分ではない。−−これでは一般性を示す範囲が分からない。
各項の位置に一般性を表す符合「A
」を導入し、たとえば「(A,A) . F(A,A)
」のようにしてみたらどうか。十分ではない。−−これらいくつかの可変項の同一性を確定できなくなる。等々。
こうした表し方すべてが不十分なのは、必要な数学的多様性に欠けているからである。
- 4.0412
- 同じ理由で、人は空間的関係を、言わば「空間めがね」越しに見るという、観念論の説明も十分なものでない。なぜならば、この説明では空間的関係がもつ多様性を説明できないからである。
- 4.05
- 現実は命題と比較される。
- 4.06
- 命題は現実の像であることによってのみ、真か偽でありえる。
- 4.061
- 命題の意義は、それが事実であるかには依存しないということを見落とすべきではない。さもないと、人は容易に、真も偽も記号とそれが表すものとの関係と同等の関係であると信じるようになる。
そのとき、例えば、「~p
」が偽なる仕方で表すものを、「p
」は真なる仕方で表すなどと言い出しかねない。等々。
- 4.062
- これまで真な命題で了解してきたように、ひとは偽な命題では了解できないのだろうか。それが偽な命題として了解されてさえいればよいのか。否。なぜなら、命題が真であるのは、事実がその命題の語るとおりであるときだからである。仮にわれわれが「
p
」で~p
のことを考えていたとしよう。しかも、事実が考えられていたとおりであったとする。そのとき、この新たな概念のもとで、「p
」は真であり、偽とはならないのである。
- 4.0621
- しかし記号「
p
」と「~p
」が同じことを語りうるということは重要である。というのも、それは記号「~
」が現実の何ものにも対応しないことを示しているのだから。
ある命題に否定が現れるということだけでは、その命題の意義を特色づけることにはならない(たとえば、~~p = p
)。
命題「p
」と「~p
」意義は反対である、しかしそれらには一つの同じ現実が対応する。
- 4.063
- 真理という概念を説明するための一つの比喩。−−白い紙の上の黒い模様。この平面上の各点に対してそこが白いか黒いかを述べていけば、それで模様の形を記述することができる。ある点が黒いという事実には肯定的事実が対応し、ある点が白い(黒くない)という事実には否定的事実が対応する。もし私が平面上の一つの点(これがフレーゲの言う真理値に対応する)を指しているとき、それは判断以前の仮定に対応する、云々。
しかし一つの点が黒いとか白いとかを語るためには、いかなる場合にある点を黒あるいは白というのか、私はあらかじめ知っていなければならない。「 P 」は真である(あるいは偽である)と語るためには、どのような状態で「 P 」を真とするのかを確定していなければならない。そしてそれによって私は命題の意義を確定するのである。
ここにおいて比喩は崩れる。−−われわれは、白とは何か黒とは何かを知らなくとも、紙の上の点を指示することができる。しかし命題は、意義を介さずには何ものにも対応しない。命題は「真」とか「偽」と呼ばれるなんらかの性質をもったあるもの(真理値)を指示するわけではないからである。命題に対して「真である」や「偽である」という動詞が与えられる、フレーゲはそう考えていたが、そうではなく、その命題が真であるということに既に「真である」という動詞が含まれているのでなくてはならない。
- 4.064
- すべての命題はあらかじめ意義をもっていなければならない。命題を肯定することによってそれに意義が与えられるのではない。肯定とはまさにその意義を肯定することであるのだから。否定等についても同様である。
- 4.0641
- 否定は、否定される命題の論理的領域にすでに関わっている、と言うこともできよう。
否定命題は否定される命題とは別の論理領域を規定する。
否定命題は、否定される命題の論理領域の助けを借りて、その外側にあると語ることによって、自らの論理的領域を規定する。
否定命題を再度否定することができる。このことは、そこで否定されるものがすでに一つの命題であり、けっして命題以前の単なる準備のようなものではないことを示している。
- 4.1
- 命題は、事態の成立と不成立を述べる。
- 4.11
- 真なる命題の全体が全自然科学(あるいは自然科学の全体)である。
- 4.111
- 哲学は自然科学ではない。
(「哲学」という語は、自然科学に並んであるのではなく、自然科学の上に、あるいは下にあるものを意味するのでなければならない。)
- 4.112
- 哲学の目的は思考の論理的明晰化である。
哲学は学説ではなく、活動である。
哲学の仕事は本質的に解明から成り立つ。
哲学の成果は「哲学的命題」ではない。諸命題が明晰になるということである。
思考は、そのままではいわば不透明でぼやけている。哲学はそれを明晰にし、はっきりとした限界を与えねばならない。
- 4.1121
- 心理学が、他の自然科学に比べて、より哲学に近いわけではない。
認識論は心理学の哲学である。
記号言語に関する私の研究は、哲学者たちが論理の哲学にとってきわめて本質的とみなしていた思考過程の研究に相当するものとなっていないだろうか。ほとんどの場合彼らは非本質的な心理学研究に絡め取られたにすぎない。そして、私の方法にも同様の危険が存在する。
- 4.1122
- ダーウィンの理論が、他の自然科学の仮説よりもより一層哲学と関係するわけではない。
- 4.113
- 哲学は自然科学の論議可能な領域に限界を与える。
- 4.114
- 哲学は思考可能なものを境界づけ、それによって思考不可能なものを境界づけなければならない。
哲学は思考可能なものを通して内側から思考不可能なものを限界づけなければならない。
- 4.115
- 哲学は、語りうるものを明晰に描写することによって、語りえぬものを指し示そうとする
- 4.116
- およそ考えられることはすべて明晰に考えられる。言い表せることはすべて明晰に言い表せる。
- 4.12
- 命題は現実のすべてを描写することができる。だが、命題は、現実を描写しうるためにそれが現実と共有しなければならないもの−−論理形式−−を描写することはできない。
論理形式を描写しうるには、われわれはその命題とともに論理の外側、すなわち世界の外側に立つことができなければならない。
- 4.121
- 命題は論理形式を描写できない。論理形式は命題に映しだされている。
言語のうちに映し出されいるものを、われわれは描写できない。
言語のうちにみずからを表現しているもの、それをわれわれが言語で表現することはできない。
命題は現実の論理形式を示す。
命題はそれを提示する。
- 4.1211
- たとえば、命題「
fa
」は、その意義の中に対象a
が現れることを示している。二つの命題「fa
」と「ga
」は、それらがともに同一の対象についての命題であることを示している。
二つの命題が互いに矛盾であるとき、このことはそれらの構造によって示されている。ある命題が他の命題から帰結するとき等々もまた、同様である。
- 4.1212
- 示されることができるものは、語られることはできない。
- 4.1213
- その中ですべてがうまくゆく、そのような記号言語さえあれば、正しい論理把握を得るに違いないという印象−−この印象もいまや理解できるのである。
- 4.122
- ある意味でわれわれは、対象や事態の形式的性質について、又事実の構造の性質について論じることができる。また同じ意味で、形式的関係や構造の関係について論じることもできる。
(構造の性質と言う代わりに、私はまた「内的性質」とも言う。そして構造の関係の代わりに「内的関係」と。
私がこうした表現を持ち込むのは、なぜかくも多くの哲学者たちが内的性質と狭義の(外的)性質を混同するのか、その理由を明らかにしたいからである。)
だが、こうした内的性質や内的関係が成立すると、命題によって主張することはできない、それはその事態を描写し、その対象を扱う命題のうちに、おのずから示される。
- 4.1221
- 事実の内的性質を、われわれはまた事実の相と呼ぶことができよう。(たとえば、人相について語るときのような意味で。)
- 4.123
- ある性質は、その対象がそれをもたないとは考えられないとき、内的性質である。
(この青色とあの青色は、おのずから、より明るい/より暗いという内的関係にある。これら二つの対象がその関係にないとは考えられない。)
(ここで「性質」や「関係」という語の用法の揺らぎに、「対象」という語の用法の揺らぎが対応している。)
- 4.124
- ある内的性質が可能的状況のうちに成り立っていることは、命題で表現されることではなく、その状況を描写する命題において、その命題の内的性質を通して、みずからを表現する。
ある命題にある形式的性質が存在すると主張することは、その否定と同様にナンセンスである。
- 4.1241
- この形式はこの性質があり、あの形式にはあの性質があると語ることによっては、諸形式を互いに区別することはできない。というのは、それぞれの性質をそれぞれの形式に帰することに意義があると前提しているから。
- 4.125
- いくつかの可能な状況の間に、ある内的関係が成り立っていることは、その状況を描写する命題間の内的関係を通して、言語のうちにみずからを表現する。
- 4.1251
- このようにして、「すべての関係は内的なのか外的なのか」という論争は解決する。
- 4.1252
- 内的関係によって順序づけられた列を、私は形式列と呼ぶ。
数列は外的関係ではなく、内的関係で順序づけられる。
以下のような命題の列も同様である。
「aRb
」、
「(∃x) : aRx . xRb
」、
「(∃x, y) : aRx . xRy . yRb
」、
等々
(b
がa
に対してこうした関係にあるとき、私はb
をa
の後継と呼ぶ。)
- 4.126
- 形式的性質という用語を用いたのと同様の意味において、いまやわれわれは形式的概念についても論じることができる。
(私が形式的概念という用語を持ち込むのは、旧来の論理学全体が形式的概念と狭義の概念との混同に貫かれているからであり、その混同の原因を明らかにするためである。)
あるものがある形式的概念にあてはまる対象の一つであるとき、そのことは命題で表現できない。しかしそれは、その対象を表すシンボルのうちに示される。(名はそれが表しているものが一つの対象であることを示す。数字はそれが表しているものが数であることを示す、等々。)
形式的概念を、狭義の概念のように関数を用いて表すことは、まったく不可能である。
なぜならば、形式的概念の特性である形式的性質は、関数で表現されないからである。
形式的性質の表現は、しかるべきシンボルの相貌である。
それゆえある形式的概念の特性を表す記号は、その概念にあてはまるすべての対象のシンボルがもつ、それらに特徴的な相貌である。
したがって、形式的概念はこの特徴的な相貌だけを定項として残した命題可変項として表現される。
- 4.127
- 命題可変項は形式的概念を表し、その値はその概念にあてはまる対象を表す。
- 4.1271
- すべての可変項は形式的概念の記号である。
なぜなら、可変項はいづれも、そのすべての値が共有する、そしてそれらの値の形式的性質とみなしうる常数的形式を表しているのだからである。
- 4.1272
- こうして、可変項名「
x
」が対象と言う擬似概念に対する本来的な記号なのである。
「対象」(「もの」「こと」等)という語が正しく使用されているかぎり、それは概念記法においては可変項名という形で表現される。
たとえば、「・・・である二つの対象がある」という命題の中では、「∃(x, y)・・・
」と表される。
それ以外の場合、すなわち固有の概念を表すものとして使用されている場合には、つねにナンセンスな擬似命題が発生する。
たとえば、「本がある」と語るように「対象がある」と語ることはできない。同様に、「百個の対象がある」とか「א0
個の対象がある」と語ることもできない。
そして全対象の総数について語ることもナンセンスである。
同じことが、「複合的なもの」「事実」「関数」「数」等々の語についてもあてはまる。
これらすべては形式的概念を表しており、概念記法では、可変項によって表され、(フレーゲやラッセルが考えたように)関数や集合によって表されるのではない。
「1
は数である」「ただ一つのゼロがある」といった表現、およびこれに類するものはすべてナンセンスである。
(「ただ一つ1
がある」と語ることは、「2 + 2
は三時には4
に等しい」と語ることと同様にナンセンスである。
- 4.12721
- 形式的概念は、それにあてはまる対象とともに、すでに与えられている。それゆえ、ある形式的概念に属する対象と、その形式的概念そのものとを、ともに基本的概念として導入することはできない。それゆえ、たとえば、(ラッセルのように)関数の概念と特定の関数とを、ともに基本概念として導入することはできない。あるいはまた、数の概念と特定の数についても同様である。
- 4.1273
- 「
b
はa
の後継である」という一般的命題を概念記法で表現しようとするならば、次の形式列の一般項を表す表現が必要となる。
aRb
、
(∃x) : aRx . xRb
、
(∃x, y) : aRx . xRy . yRb
、
等々
形式列の一般項は可変項によってのみ表現できるが、それは「この形式列の一般項」という概念が形式的概念であるからである。(このことをフレーゲとラッセルは見落とした。そのため、こうした一般命題を表現しようとして彼らが取った方法は間違っている。それは悪循環を含んでいる。)
われわれは、その形式列の初項を示し、かつ、先行する命題をもとに後継の項を作り出す操作の一般形式を示すことによって、この形式列の一般項を規定することができる。
- 4.1274
- 形式的概念の存在を問うことはナンセンスである。いかなる命題もそのような問いに答えることはできないからである。
(たとえば「分析不可能な主語−述語命題は存在するか」と問うことはできない。)
- 4.128
- 論理形式には数の概念がない。
それゆえ論理には卓越した数は存在しない。したがって哲学的一元論、二元論、等々は存在しえない。
- 4.2
- 命題の意義とは、事態の成立・不成立の可能性と、その命題との一致・不一致である。
- 4.21
- もっとも単純な命題、すなわち要素命題は、ある事態の成立を主張する。
- 4.211
- 要素命題の特徴は、いかなる要素命題もそれと相反することがないことである。
- 4.22
- 要素命題は名から成り立つ。それはいくつかの名の結合・連鎖である。
- 4.221
- 明らかに、命題を分析していけば名が直接結合してできた要素命題に行きつかねばならない。
ここにおいて、いかにして命題と命題の結合が為されるのかという問が生じる。
- 4.2211
- たとえ世界が無限に複合的で、どの事実も無限に多くの事態からなり、事態もまたすべて無限に多くの対象から構成されていたとしても、それでもなお対象と事態は存在していなければならない。
- 4.23
- 名は、要素命題の文脈においてのみ、命題に現れる。
- 4.24
- 名は単一なシンボルである。私は、それを個々の文字(「
x
」、「y
」、「z
」)で表す。
要素命題を私は、名の函数として、「fx
」, 「φ
(x
、y
)」 等の形式で書く。
あるいは、p
、q
、r
という文字でも表す。
- 4.241
- 二つの記号を一つの同じ意味で使用する場合、私は両者の間に記号 「
=
」 をおくことによって表現する。
それゆえ 「a = b
」 は、記号 「a
」 は記号 「b
」 で置き換え可能ということである。
(私が、等式によって新しい記号 「b
」 を導入し、その記号を既知の記号 「a
」 と置き換えるべきものと決めるとき、私はその等式−−定義−−を(ラッセルにならって) 「定義 a = b
」 という形式で書く。定義とは、記号の使用規則である。)
- 4.242
- それゆえ、 「
a = b
」 という形式の表現は、描写の為の仕掛けにすぎない。それは記号 「a
」 「b
」 の意味については何も語らない。
- 4.243
- 二つの名が同じものを表しているのか、それとも異なるものを表しているのかを知らずに、それらを理解できるだろうか?−−同じ意味なのか異なる意味なのか分からない二つの名を含む命題を、われわれは理解できるだろうか?
ある英単語の意味を把握しており、またそれと同義のドイツ語単語の意味も把握しているならば、両者が同じ意味であると知らないことはありえない。それらを相互に翻訳できないということなどありえない。
「a = a
」 のような表現、又そこから導かれる表現は、要素命題ではないし、それ以外の何か有意義な記号でもない。(この点は後述する。)
- 4.25
- 要素命題が真ならば、事態は成立している。偽の時、事態は成立していない。
- 4.26
- すべての真な要素命題を挙げれば、世界は完全に記述される。すべての要素命題を挙げ、さらに、そのいずれが真で、いずれが偽であるかを述べれば、世界は完全に記述される。
- 4.27
n
個の事態の成立・不成立にかんして、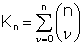 通りの可能性がある。
通りの可能性がある。
どの事態の組み合わせも成り立ち、そして他の組み合わせはなりたたないということが可能である。
- 4.28
- これらの事態の組み合わせに、
n
個の要素命題の真−−および偽−−の可能性が、同じ数だけ対応している。
- 4.3
- 要素命題の真理可能性とは、事態の成立・不成立の可能性を意味している。
- 4.31
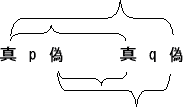
- 真理可能性は次のような図表で表すことができる。(要素命題の行にある「真」と「偽」は、要素命題の真理可能性を分かりやすく表したものである。)
p
真 偽
p
真 偽 真 偽 q
真 真 偽 偽
p
真 偽 真 真 偽 偽 真 偽 q
真 真 偽 真 偽 真 偽 偽 r
真 真 真 偽 真 偽 偽 偽
- 4.4
- 命題とは、その要素命題の真理可能性との、一致・不一致の表現である。
- 4.41
- 要素命題の真理可能性が命題の真・偽の条件である。
- 4.411
- 直ちに確かなものと予期されるが、要素命題の導入が他のすべての種類の命題を理解するための基礎を与える。確かに、一般命題の理解は歴然として要素命題の理解に依存している。
- 4.42
- ある命題が
n
個の要素命題の真理可能性のどれと一致し、どれと一致しないかは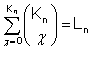 の可能性がある。
の可能性がある。
- 4.43
- 真理可能性との一致は、図表のその真理可能性に「真」という符号を添えることにより表現することができる。
この符号がなければ、不一致を意味する。
- 4.431
- 要素命題の真理可能性との一致および不一致の表現が、その命題の真理条件を表す。
命題はその真理条件の表現である。
(それゆえフレーゲが彼の概念記法の記号の説明としてまず真理条件を与えたことは、完全に正しかった。ただし、フレーゲの真理概念の説明はまちがっている。フレーゲの言うように「真」「偽」が対象であり、~p
等々における入出力項であるとするならば、フレーゲの規定に従うと、「~p
」 の意味はまったく定まらないことになる。)
- 4.44
- 真理可能性に[真」という符号を添えて作られる記号が命題記号である。
- 4.441
- 明らかに、記号「偽」および「真」の複合はいかなる対象にも(対象の複合にも)対応しない。同様に水平線と垂直線、あるいは括弧も対象に対応しない。−−「論理的対象」は存在しない。
もちろん「真」と「偽」の図表と同じことを表現する記号についても、同様である。
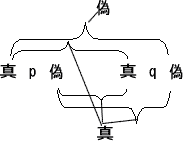
- 4.442
- 例えば
「
」 は命題記号である。p
真 偽 真 偽 q
真 真 偽 偽
真 真 真
(フレーゲの「判断線」「|-
」は論理的にはまったく意味をもたない。それはフレーゲ(そしてラッセル)において、ただ彼らがこの記号のついた命題を真とみなしていることを表すにすぎない。「|-
」はそれゆえ、命題に付された番号と同様、命題の一部ではない。命題が自分自信について真であると語ることはできない。)
図表における真理可能性の行の並び方を組み合わせ規則によってあらかじめすべて決定しておけば、最終列だけで真理条件の一組を表現するには十分である。そこでこの列を書き出せば、その命題記号は次のようなものになる。
「(真真−真)(p
,q
)」
あるいは、より明示的に
「(真真偽真)(p
,q
)」。
(左の括弧内の項の数は右の括弧内の項数に応じて決まる。)
- 4.45
n
個の要素命題にたいして、Ln
個の真理条件の組が可能である。
一連の要素命題の真理可能性から得られる真理条件の組は、順序をつけて配列できる。
- 4.46
- 真理条件の可能な組の中に、二つの極端な場合がある。
ひとつは、要素命題のすべての真理可能性に対してその命題は真となる。このとき、この真理条件の組はトートロジー的であるという。
もうひとつは、すべての真理可能性に対してその命題は偽となる。この真理条件の組は矛盾的である。
第一の場合、その命題はトートロジーと呼ばれ、第二の場合には矛盾と呼ばれる。
- 4.461
- 命題はそれが語っていることを示しているが、トートロジーと矛盾は、それが何も語らないことを示している。
トートロジーは無条件に真であり、従って真理条件をもたない。そして、矛盾は真となる条件をもたない。
トートロジーと矛盾は無意義である。
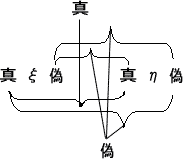
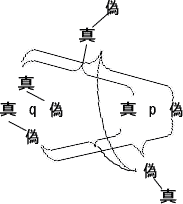
(それは、二本の矢が反対の方向に飛び去ったあとの点のようである。)
(たとえば、今雨が降っているか降っていないかどちらかであると知っていても、私が天気について何か知っていることにはならない。)
- 4.4611
- しかしトートロジーと矛盾はナンセンスではない。それらは、「
0
」が算術の記号体系の一部であるように、記号体系の一部である。
- 4.462
- トートロジーと矛盾は現実に対する像ではない。それは可能な状況を描写しない。前者は可能な状況をすべて許容し、後者はまったく許容しない。
トートロジーでは、世界との一致の条件−−描写の関係−−が互いに打ち消しあい、その結果、現実といかなる描写の関係にも立たなくなる。
- 4.463
- 真理条件は、その命題が事実に許容する可能な範囲を規定する。
(命題、像、模型、これらは、否定的な意味では、相互の運動の自由を制限する固体のようであり、肯定的意味では、物体が位置を占めうる、実体で囲まれた空間のようである。)
トートロジーは、現実がありうる位置として論理空間の全体を−−無限に−−許容する。矛盾は、論理空間全体を埋め尽くし、現実に場所を残さない。それゆえ、どちらも決して現実を規定できない。
- 4.464
- トートロジーが真であることは確実であり、命題のそれは可能、矛盾のそれは不可能である。
(確実、可能、不可能−−確率論に必要とされる概念の最初の兆しがここにある。)
- 4.465
- トートロジーと命題との論理積はその命題と同じことを語る。それゆえその論理積はその命題と同一である。というのは、シンボルの意義を変えること無しに、シンボルにとって本質的なものを変えることはできないからである。
- 4.466
- 記号を特定の仕方で論理的に結合したものは、その記号の意味を特定の仕方で論理的に結合したものに対応する。すべての任意的結合には、結合されていない記号だけが対応する。
言いかえると、いかなる状況に対しても真となる命題は、およそ記号の結合ではありえない。そうでなければ、それらの命題には対象の特定の結合だけが対応しているはずであるから。
(そして、論理的結合でないものには、それに対応する対象の結合もまた存在しない。)
トートロジーと矛盾は記号結合の極限的事例である。すなわち、記号結合の解消である。
- 4.4661
- もちろん、トートロジーや矛盾のなかでも記号は互いに結合されている、すなわち、記号は相互に関係している。しかしこの関係は意味を持っていない、それはシンボルにとっては非本質的なのである。
- 4.5
- いまや、もっとも普遍的な命題形式を示すことができると思われる。いいかえると、なんらかの記号言語によって命題とはいかなるものであるのかを記述することが可能であると思われる。そのとき、名の指示対象を適切に選んでやれば、全ての可能な意義は、その記述にあてはまる記号によって表現することができ、また、その記述にあてはまる記号はすべて、相応の意義を表現しうることになる。
明らかに、もっとも普遍的な命題形式の記述においては、その本質的なものだけが記述されなければならない。−−さもなければ、その形式はもっとも普遍的なものではないことになる。
予見(すなわち構成)不可能な形式をもつ命題は存在しえない。このことは、普遍的な命題形式が存在することを示している。
「ものごとはしかじかである。」−−これが命題の普遍的形式である。