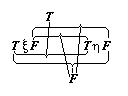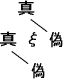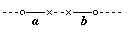英1 The logical picture of the facts is the thought.
英2 A logical picture of facts is a thought.
日 事実の論理像*が思考である。
英1 "An atomic fact is thinkable" -- means: we can imagine it.
英2 'A state of affairs is thinkable': what this means is that we can picture it to ourselves.
日 「ある事態が思考可能である」とは、その事態の像を描くことができるということを意味する。
英1 The totality of true thoughts is a picture of the world.
英2 The totality of true thoughts is a picture of the world.
日 真である思考の全体が、世界の像である。
英1 The though contains the possibility of the state of affairs which it thinks.
What is thinkable is also possible.
英2 A thought contains the possibility of the situation of which it is the thought. What is thinkable is possible too.
日 思考は、考えている状況が可能であることを含んでいる。考えられることはまた可能なことでもある。
英1 We cannot think anything unlogical, for otherwise we should have to think unlogically.
英2 Thought can never be of anything illogical, since, if it were, we should have to think illogically.
日 非論理的なことを考えることはできない。さもなければ、非論理的に思考しなければならなくなるだろう。
英1 It used to be said that God could create everything, except what was contrary to the laws of logic. The truth is, we could not say of an "unlogical" world how it would look.
英2 It used to be said that God could create anything except what would be contrary to the laws of logic.The truth is that we could not say what an'illogical' world would look like.
日 神はすべてを創造しうる。ただ論理法則に反することを除いては、とかって言われていた。--実際、「非論理的」世界がどのようであるかなど、語りえないのである。
英1 To present in language anything which "contradicts logic" is as impossible as in geometry to present by its co-ordinates a figure which contradicts the laws of space; or to give the co-ordinates of a point which does not exist.
英2 It is as impossible to represent in language anything that'contradicts logic' as it is in geometry to represent by its coordinates a figure that contradicts the laws of space, or to give the coordinates of a point that does not exist.
日 「論理に反する」ことは言語で描写できない。それは、幾何学において、空間の法則に反する図形を座標で描写したり、存在しない点の座標を示すことができないのと同様である。
英1 We could present spatially an atomic fact which contradicted the laws of physics, but not one which contradicted the laws of geometry.
英2 Though a state of affairs that would contravene the laws of physics can be represented by us spatially, one that would contravene the laws of geometry cannot.
日 たしかに、物理法則に反した事態を空間的に描写することはできるだろう。しかし、幾何法則に反した事態は空間的には描写できない。
英1 An a priori true thought would be one whose possibility guaranteed its truth.
英2 It a thought were correct a priori, it would be a thought whose possibility ensured its truth.
日 ア・プリオリに正しい思考とは、思考の可能性がその真を保証する、そのような思考であるだろう。
英1 Only if we could know a priori that a thought is true if its truth was to be recognized from the thought itself (without an object of comparison).
英2 A priori knowledge that a thought was true would be possible only it its truth were recognizable from the thought itself (without anything a to compare it with).
日 思考そのものから(比較の対象無しに)真であることがわかる、そのような思考にかぎり、ア・プリオリに真であることを知りうるであろう。
英1 In the proposition the thought is expressed perceptibly through the senses.
英2 In a proposition a thought finds an expression that can be perceived by the senses.
日 思考は命題において、感性的に知覚可能な表現となる。
Die Projektionsmethode ist das Denken des Satz-Sinnes.
英1 We use the sensibly perceptible sign (sound or written sign, etc.) of the proposition as a projection of the possible state of affairs.
The method of projection is the thinking of the sense of the proposition.
英2 We use the perceptible sign of a proposition (spoken or written, etc.) as a projection of a possible situation. The method of projection is to think of the sense of the proposition.
日 われわれは、可能な状況の投影として、命題を表す知覚可能な記号(音声記号、文字記号、等々)を用いる。
投影の方法は、命題--意義を考えることである。
英1 The sign through which we express the though I call the proposition sign. And the proposition is the proposition sign in its projective relation to the world.
英2 I call the sign with which we express a thought a propositional sign.And a proposition is a propositional sign in its projective relation to the world.
日 われわれが思考を表現するために用いる記号を、私は命題記号とよぶ。すなわち、命題とは、世界に対し投影的に関係している命題記号である。
Also die Möglichkeit des Projizierten, aber nicht dieses selbst.
Im Satz ist also sein Sinn noch nicht enthalten, wohl aber die Möglichkeit, ihn auszudrücken.
(»Der Inhalt des Satzes« heißt der Inhalt des sinnvollen Satzes.)
Im Satz ist die Form seines Sinnes enthalten, aber nicht dessen Inhalt.
英1 To the proposition belongs everything which belongs to the projection; but not what is projected.
Therefore the possibility of what is projected but not this itself.
In the proposition, therefore, its sense is not yet contained, but the possibility of expressing it.
("The content of the proposition" means the content of the signicant proposition.)
In the proposition the form of its sense is contained, but not its content.
英2 A proposition, therefore, does not actually contain its sense, but does contain the possibility of expressing it. ('The content of a proposition' means the content of a proposition that has sense.) A proposition contains the form, but not the content, of its sense.
日 投影に属するすべては、命題に属する。しかし、投影されていることは命題に属さない。
すなわち、命題に属するのは、投影されていることの可能性であり、投影されていることそれ自身ではない。
それゆえ、命題にはその意義までは含まれていない。しかしそれを表現する可能性は含まれている。
(「命題の内容」とは、有意義な命題の内容である。)
命題に含まれるのは意義の形式であり、内容ではない。
Das Satzzeichen ist eine Tatsache.
英1 The propositional sign consists in the fact that its elements, the words, are combined in it in a definite way.
The propositional sign is a fact.
英2 What constitutes a propositional sign is that in its elements (the words) stand in a determinate relation to one another. A propositional sign is a fact.
日 命題記号は、その要素、すなわち語が特定の仕方でたがいに関係するところになりたつ。
命題記号はひとつの事実である。
Der Satz ist artikuliert.
英1 The proposition is not a mixture of words (just as the musical theme is not a mixture of tones).
The proposition is articulate.
英2 A proposition is not a blend of words.(Just as a theme in music is not a blend of notes.) A proposition is articulate.
日 命題は語の寄せ集めではない。--(音楽の主題が音の寄せ集めではないように。)
命題は語に分節化されている。
英1 Only facts can express a sense, a class of names cannot.
英2 Only facts can express a sense, a set of names cannot.
日 ただ事実だけが意義を表現することができる、名の集まりでは表現できない。
Denn im gedruckten Satz z.B. sieht das Satzzeichen nicht wesentlich verschieden aus vom Wort.
(So war es möglich, dass Frege den Satz einen zusammengesetzten Namen nannte.)
英1 That the propositional sign is a fact is concealed by the ordinary form of expression, written or printed.
For in the printed proposition, for example, the sign of a proposition does not appear essentially different from a word. (Thus it was possible for Frege to call the proposition a compounded name.)
英2 Although a propositional sign is a fact, this is obscured by the usual form of expression in writing or print. For in a printed proposition,for example, no essential difference is apparent between a propositional sign and a word. (That is what made it possible for Frege to call aproposition a composite name.)
日 命題記号がひとつの事実であることは、手書き文字や活字という通常の表現形態によって見えにくくなっている。
たとえば印刷された命題では、命題記号は語と本質的な区別があるようには見えない。(それゆえ、フレーゲは命題を合成された名と呼ぶことができたのである。)
Die gegenseitige räumliche Lage dieser Dinge drückt dann den Sinn des Satzes aus.
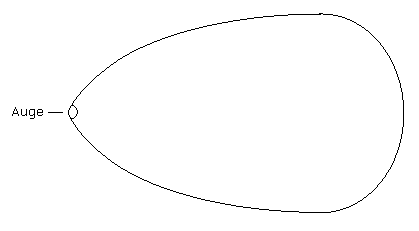
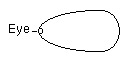
英1 The essential nature of the propositional sign becomes very clean when we imagine it made up of spatial objects (such as tables, chairs, books) instead of written signs.
The mutual spatial position of these things then expresses the sense of the proposition.
英2 The essence of a propositional sign is very clearly seen if we imagine one composed of spatial objects (such as tables, chairs, and books)instead of written signs.
日 命題記号が文字ではなく、(机、椅子、本といった)空間的な対象から構成されると考えてみれば、命題記号の本質がきわめてはっきりするだろう。
そこでは、これらのもの相互の空間的配置が命題の意義を表現する。
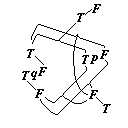
英1 We must not say, "The complex sign `aRb' says `a stands in relation R to b'"; but we must says, "That `a' stands in a certain relation to `b' says that aRb".
英2 Instead of, 'The complex sign "aRb" says that a stands to b in the relation R' we ought to put, 'That "a" stands to "b" in a certain relation says that aRb.'
日 『複合記号「
aRb」は、a が b に対して関係 R にあることを語っている。』のではなく、「a」が「b」に対してなんらかの関係にあるということが、 aRb ということを語っているのである。
(Namen gleichen Punkten, Sätze Pfeilen, sie haben Sinn.)
英1 States of affairs can be described but not named.
(Names resemble points; propositions resemble arrows, they have senses.)
英2 Situations can be described but not given names.
日 状況は記述することができるが、名指しすることはできない。
(名は点に似ている。命題は矢に似ている、ともに意義・方向をもつ。)
英1 In propositions thoughts can be so expressed that to the objects of the thoughts correspond the elements of the propositional sign.
英2 In a proposition a thought can be expressed in such a way that elementsof the propositional sign correspond to the objects of the thought.
日 思考の対象に命題記号*の要素が対応する。そのような仕方で、思考は命題のうちに表現される。
英1 These elements I call "simple signs" and the proposition "completely analysed".
英2 I call such elements 'simple signs', and such a proposition 'complete analysed'.
日 この要素を私は「単純記号」と呼び、そしてこの命題は「完全に分析された」と言う。
英1 The simple signs employed in propositions are called names.
英2 The simple signs employed in propositions are called names.
日 命題の中で用いられた単純記号は名と呼ばれる。
英1 The name means the object. The object is its meaning. ("A" is the same sign as "A".)
英2 A name means an object. The object is its meaning. ('A' is the same sign as 'A'.)
日 名は対象を意味する。対象が名の意味である。(「
A]は「A」と同じ記号である)
英1 To the configuration of the simple signs in the propositional sign corresponds the configuration of the objects in the state of affairs.
英2 The configuration of objects in a situation corresponds to the configuration of simple signs in the propositional sign.
日 命題記号における単純記号*の配置に、状況における対象の配置が対応する。
英1 In the proposition the name represents the object.
英2 In the proposition the name represents the object.
日 名*は命題のなかで対象を代理する。
英1 Objects I can only name. Signs represent them. I can only speak of them. I cannot assert them. A proposition can only say howa thing is, not what it is.
英2 Objects can only be named. Signs are their representatives. I can only speak about them: I can not put them into words. Propositions can only say how things are, not what they are.
日 対象はただ名づけることができるだけである。そして記号は対象を代理する。私は対象について語ることはできるが、対象そのものを語ることはできない。命題はただものがいかにあるかを語ることができるだけであり、それが何であるかを語ることはできない。
英1 The postulate of the possibility of the simple signs is the postulate of the determinateness of the sense.
英2 The requirement that simple signs be possible is the requirement that sense be determinate.
日 単純記号が可能でなければならないという要請は、命題の意義が確定しなければならないという要請である。
Der Komplex kann nur durch seine Beschreibung gegeben sein, und diese wird stimmen oder nicht stimmen. Der Satz, in welchem von einem Komplex die Rede ist, wird, wenn dieser nicht existiert, nicht unsinnig, sondern einfach falsch sein.
Dass ein Satzelement einen Komplex bezeichnet, kann man aus einer Unbestimmtheit in den Sätzen sehen, worin es vorkommt. Wir wissen, durch diesen Satz ist noch nicht alles bestimmt. (Die Allgemeinheitsbezeichnung enthält ja ein Urbild.)
Die Zusammenfassung des Symbols eines Komplexes in ein einfaches Symbol kann durch eine Definition ausgedrückt werden.
英1 A proposition about a complex stands in internal relation to the proposition about its consituent part.
A complex can only be given by its description, and this will either be right or wrong. The propostion in which there is mention of a complex, if this does not exist, becomes not nonsense but simply false.
That a propositional element signifies a complex can be seen from an indeterminateness in the propositions in which it occurs. We know that everything is not yet determined by this proposition. (The notation for generality contains a prototype.)
The combination of the symbols of a complex in a simple symbol can be expressed by a definition.
英2 A proposition about a complex stands in an internal relation to a proposition about a constituent of the complex. A complex can be given only by its description, which will be right or wrong. A proposition that mentions a complex will not be nonsensical, if the complex does not exits, but simply false. When a propositional element signifies a complex, this can be seen from an indeterminateness in the propositions in which it occurs. In such cases we know that the proposition leaves something undetermined. (In fact the notation for generality contains a prototype.) The contraction of a symbol for a complex into a simple symbol can be expressed in a definition.
日 複合的なものをあつかう命題は、その構成部分をあつかう命題と内的な関係にある。
複合的なものは、その記述によってのみ与えられうる。そしてその記述は正しいか正しくないかのいずれかである。複合的なものに言及する命題は、その複合的なものが存在しない場合、ナンセンスではなく、ただたんに偽となる。
命題のある要素が複合的なものを表示していることは、その要素を含む命題の不確定性から見て取れる。われわれはこの命題では、まだすべてが確定しているわけではないことを知る。(一般性の表記はプロトタイプを含んでいる。)
複合的なものを表すシンボル*の組み合わせを一つの単純なシンボルに要約することが、定義によって可能である。
英1 There is one and only one complete analysis of the proposition.
英2 There is one and only one complete analysis of the proposition.
日 命題の完全な分析が、一つそして唯一つ存在する。
英1 The proposition expresses what it expresses in a definite and clearly specifiable way: the proposition is articulate.
英2 The proposition expresses what it expresses in a definite and clearly specifiable way: the proposition is articulate.
日 命題は、その表現していることを、確定した、明確に指定しうる仕方で表現する。すなわち、命題は分節化されている。
英1 The name cannot be analysed further by any definition. It is a primitive sign.
英2 The name cannot be analysed further by any definition. It is a primitive sign.
日 どのような定義によっても、名はそれ以上分解することができない。名は原始記号である。
Zwei Zeichen, ein Urzeichen, und ein durch Urzeichen definiertes, können nicht auf dieselbe Art und Weise bezeichnen. Namen kann man nicht durch Definitionen auseinanderlegen. (Kein Zeichen, welches allein, selbständig eine Bedeutung hat.)
英1 Every defined sign signifies via those signs by which it is defined, and the definitions show the way.
Two signs, one a primitive sign, and one defined by primitive signs, cannot signify in the same way. Names cannot be taken to pieces by definition (nor any sign which alone and independently has a meaning).
英2 Every sign that has a definition signifies via the signs that serve to define it; and the definitions point the way. Two signs cannot signify in the same manner if one is primitive and the other is defined by means of primitive signs. Names cannot be anatomized by means of definitions. (Nor can any sign that has a meaning independently and on its own.)
日 定義された記号はすべて、その定義に用いられた記号を経由して表示する。定義はそうして道を示す。
原始記号および原始記号によって定義された記号、この二種の記号が同じ仕方でものを表示することはできない。名を定義によって他の記号に分解することはできない。(それだけで独立に意味をもつ記号を、定義によって他の記号に分解することはできない。)
英1 What does not get expressed in the sign is shown by its application. What the signs conceal, their application declares.
英2 What signs fail to express, their application shows. What signs slur over, their application says clearly.
日 記号で表現されていないことが、記号の使用によって示される。その記号が隠しているものを、記号の使用が現す。
英1 The meanings of primitive signs can be explained by elucidations. Elucidations are propositions which contain the primitive signs. They can, therefore, only be understood when the meanings of these signs are already known.
英2 The meanings of primitive signs can be explained by means of elucidations. Elucidations are propositions that stood if the meanings of those signs are already known.
日 原始記号の意味は解明によって明らかにすることができる。解明とはその原始記号を使用している諸命題である。それゆえそれら原始記号の意味が既に知られている時にのみ、解明を理解することができる。
英1 Only the proposition has sense; only in the context of a proposition has a name meaning.
英2 Only propositions have sense; only in the nexus of a proposition does a name have meaning.
日 命題だけが意義をもつ。命題の文脈においてのみ、名*は意味をもつ。
(Der Satz selbst ist ein Ausdruck.)
Ausdruck ist alles, für den Sinn des Satzes Wesentliche, was Sätze miteinander gemein haben können.
Der Ausdruck kennzeichnet eine Form und einen Inhalt.
英1 Every part of a proposition which characterizes its sense I call an expression (a symbol).
(The proposition itself is an expression.)
Expressions are everything -- essential for the sense of the proposition -- that propositions can have in common with one another.
An expression characterizes a form and a content.
英2 I call any part of a proposition that characterizes its sense an expression (or a symbol). (A proposition is itself an expression.) Everything essential to their sense that propositions can have in common with one another is an expression. An expression is the mark of a form and a content.
日 命題の意義を特徴づけているその構成要素すべてを、私は表現(シンボル)と呼ぶ。
(命題自身が一つの表現である)
命題の意義にとって本質的で、命題が互いに共有できるもの、そういうものすべてが表現である。
表現は命題の形式と内容を特徴づける。
英1 An expression presupposes the forms of all propositions in which it can occur. it is the common characteristic mark of a class of propositions.
英2 An expression presupposes the forms of all the propositions in which it can occur. It is the common characteristic mark of a class of propositions.
日 表現は、その表現が現れることのできるすべての命題の形式を前提とする。表現は、それを含む命題の集合を特徴づける共通の目印である。
Und zwar wird in dieser Form der Ausdruck konstant und alles übrige variabel sein.
英1 It is therefore represented by the general form of the propositions which it characterizes.
And in this form the expression is constant and everything else variable.
英2 It is therefore presented by means of the general form of the propositions that it characterizes. In fact, in this form the expression will be constant and everything else variable.
日 したがって表現は、それが特徴づける諸命題の一般形式によって表される。
この一般形式において、その表現は定項となり、他のすべては可変項となる。
Ich nenne eine solche Variable »Satzvariable«.
英1 An expression is thus presented by a variable, whose values are the propositions which contain the expression.
(In the limiting case the variable becomes constant, the expression a proposition.)
I call such a variable a "propositional variable".
英2 Thus an expression is presented by means of a variable whose values are the propositions that contain the expression. (In the limiting case the variable becomes a constant, the expression becomes a proposition.) I call such a variable a 'propositional variable'.
日 それゆえ、表現は可変項を用いて表される。その値はその表現を含む命題である。
(極端な場合、命題全体が表現となり、そのとき可変項は定項になる。)
命題を値とするこのような可変項を、私は「命題可変項」と呼ぶ。
(Auch der variable Name.)
英1 An expression has meaning only in a proposition. Every variable can be conceived as a propositional variable.
(Including the variable name.)
英2 An expression has meaning only in a proposition. All variables can be construed as propositional variables. (Even variable names.)
日 表現は命題の中でのみ意味をもつ。すべての可変項は命題可変項として解釈できる。
(名の可変項も同様。)
英1 If we change a constituent part of a proposition into a variable, there is a class of propositions which are all the values of the resulting variable proposition. This class in general still depends on what, by arbitrary agreement, we mean by parts of that proposition. But if we change all those signs, whose meaning was arbitrarily determined, into variables, there always remains such a class. But this is now no longer dependent on any agreement; it depends only on the nature of the proposition. It corresponds to a logical form, to a logical prototype.
英2 If we turn a constituent of a proposition into a variable, there is a class of propositions all of which are values of the resulting variable proposition. In general, this class too will be dependent on the meaning that our arbitrary conventions have given to parts of the original proposition. But if all the signs in it that have arbitrarily determined meanings are turned into variables, we shall still get a class of this kind. This one, however, is not dependent on any convention, but solely on the nature of the proposition. It corresponds to a logical form--a logical prototype.
日 ある命題の一つの構成要素を可変項に変えると、可変的命題になり、その可変的命題の値となる命題全体の集合が生じる。この集合は、一般的には、われわれが命題の構成部分にどういう意味を与えるかという恣意的取り決めにまだ依存している。しかし、意味が恣意的に決められるそうした記号をすべて可変項にしてしまっても、それでも依然としてその値となる命題の集合が一つ存在する。もはやその集合はいかなる取り決めにも依存せず、ただ命題の本性のみに依存している。この命題の集合は、論理形式--論理的プロトタイプ--に対応する。
Die Festsetzung der Werte ist die Variable.
英1 What values the propositional variable can assume is determined.
The determination of the values is the variable.
英2 What values a propositional variable may take is something that is stipulated. The stipulation of values is the variable.
日 命題可変項がいかなる値を取りうるかは規定されている。この値の規定が、すなわちその可変項である。
Die Festsetzung ist eine Beschreibung dieser Sätze.
Die Festsetzung wird also nur von Symbolen, nicht von deren Bedeutung handeln.
Und nur dies ist der Festsetzung wesentlich, dass sie nur eine Beschreibung von Symbolen ist und nicht über das Bezeichnete aussagt.
Wie die Beschreibung der Sätze geschieht, ist unwesentlich.
英1 The determination of the values of the propositional variable is done by indicating the propositions whose common mark the variable is.
The determination is a description of these propositions.
The determination will therefore deal only with symbols not with their meaning.
And only this is essential to the determination, that is is only a description of symbols and asserts nothing about whiat is symbolized.
The way in which we describe the propositions is not essential.
英2 To stipulate values for a propositional variable is to give the propositions whose common characteristic the variable is. The stipulation is a description of those propositions. The stipulation will therefore be concerned only with symbols, not with their meaning. And the only thing essential to the stipulation is that it is merely a description of symbols and states nothing about what is signified. How the description of the propositions is produced is not essential.
日 命題可変項の値を規定することは、この可変項を共通の目印とする命題を列挙することである。
値を規定するとは、それらの命題を記述することである。
それゆえに、値を規定することはただシンボルにのみ関わり、その意味には関わらない。
値の規定がシンボルの記述にすぎず、そのシンボルが何を表示しているかには関わらないということ、値の規定にとって本質的なのはこのことだけである。
われわれがその命題をどう記述するかは本質的ではない。
英1 I conceive the proposition -- like Frege and Russell -- as a function of the expressions contained in it.
英2 Like Frege and Russell I construe a proposition as a function of the expressions contained in it.
日 私は--フレーゲやラッセルと同様--命題をそれに含まれている諸表現の関数であると捉える。
英1 The sign is the part of the symbol perceptible by the senses.
英2 A sign is what can be perceived of a symbol.
日 記号はシンボルの知覚可能な側面である。
英1 Two different symbols can therefore have the sign (the written sign or the sound sign) in common -- they then signify in different ways.
英2 So one and the same sign (written or spoken, etc.) can be common to two different symbols--in which case they will signify in different ways.
日 それゆえ二つの異なるシンボルが同じ記号(文字、音声、等々)を共有することがありうる。そのときそれら二つの異なるシンボルは、同じ記号だが、異なった仕方で表示する。
英1 It can never indicate the common characteristic of two objects that we symbolize them with the same signs but by different methods of symbolizing. For the sign is arbitrary. We could therefore equally well choose two different signs and where then would be what was common in the symbolization.
英2 Our use of the same sign to signify two different objects can never indicate a common characteristic of the two, if we use it with two different modes of signification. For the sign, of course, is arbitrary. So we could choose two different signs instead, and then what would be left in common on the signifying side?
日 二つの対象を同じ記号で表示したからといって、その記号化作用の仕方が異なる以上、それをもって二つの対象に共通の特徴を示したことにはならない。なぜならば、記号は恣意的だからである。それゆえ、二つの異なる対象に対して二つの異なる記号を選ぶことも可能である。そうしたとき、表示における共通の見かけの何が残るだろうか。
So erscheint das Wort »ist« als Kopula, als Gleichheitszeichen und als Ausdruck der Existenz; »existieren« als intransitives Zeitwort wie »gehen«; »identisch« als Eigenschaftswort; wir reden von Etwas, aber auch davon, dass etwas geschieht.
(Im Satze »Grün ist grün« - wo das erste Wort ein Personenname, das letzte ein Eigenschaftswort ist - haben diese Worte nicht einfach verschiedene Bedeutung, sondern es sind verschiedene Symbole.)
英1 In the language of everyday life it very often happens that the same word signifies in two different ways -- and therefore belongs to two different symbols -- or that two words, which signify in different ways, are apparently applied in the same way in the proposition.
Thus the word "is" appears as the copula, as the sign of equality, and as the expression of existence; "to exist" as an intransitive verb like "to go"; "identical" as an adjective; we speak of something but also of the fact of something happening.
(In the proposition "Green is green" -- where the first word is a proper name as the last an adjective -- these words have not merely different meanings but they are different symbols.)
英2 In everyday language it very frequently happens that the same word has different modes of signification--and so belongs to different symbols--or that two words that have different modes of signification are employed in propositions in what is superficially the same way. Thus the word 'is' figures as the copula, as a sign for identity, and as an expression for existence; 'exist' figures as an intransitive verb like 'go', and 'identical' as an adjective; we speak of something, but also of something's happening. (In the proposition, 'Green is green'--where the first word is the proper name of a person and the last an adjective--these words do not merely have different meanings: they are different symbols.)
日 日常言語では、同じ語が異なった仕方で表示する--つまり同じ語が異なったシンボルに属する--ことがきわめて多い。あるいはまた、異なった仕方で表示する二つの語が外見上は同じ仕方で命題中に用いられることもある。
たとえば ’ist’[・・である、・・がある]という語は、繋辞として、等号として、あるいは存在の表示として、用いられる。「存在する」は「行く」のような自動詞として、「同じ」は形容詞として扱われる。’etwas’[何ものか、何ごとか]という語で、われわれは何かある対象についても語り、また何かあるできごとが起きると語ったりもする。
(「緑は緑である」という命題--初めの語は人名であり、あとの語は形容詞である--において、これらの言葉はたんに意味が違うだけでなく、それぞれが異なったシンボルなのである。)
英1 Thus there easily arise the most fundamental confusions (of which the whole of philosophy is full).
英2 In this way the most fundamental confusions are easily produced (the whole of philosophy is full of them).
日 こうして、もっとも基本的な混同が容易に発生する。(哲学全体がこうした混同に満ちている。)
(Die Begriffsschrift Freges und Russells ist eine solche Sprache, die allerdings noch nicht alle Fehler ausschließt.)
英1 In order to avoid these errors, we must employ a symbolism which exlucdes them, by not applying the same sign in different symbols and by not applying signs in the same way which signify in different ways. A symbolism, that is to say, which obeys the rules of logical grammar -- of logical syntax.
(The logical symbolism of Frege and Russell is such a language, which, however, does still not exclude all errors.)
英2 In order to avoid such errors we must make use of a sign-language that excludes them by not using the same sign for different symbols and by not using in a superficially similar way signs that have different modes of signification: that is to say, a sign-language that is governed by logicalgrammar--by logical syntax. (The conceptual notation of Frege and Russellis such a language, though, it is true, it fails to exclude all mistakes.)
日 こうした誤りを避けるために、異なるシンボルに同じ記号が使用されたり、表示の仕方の異なる記号が同じ仕方で使用されることのない、誤りを排した記号言語、すなわち、論理的文法--論理的構文論--による記号言語を用いなければならない。
(フレーゲとラッセルの概念記法はそのような言語である。しかしそれはまだ全ての誤りを排除できてはいない。)
英1 In order to recognize the symbol in the sign we must consider the significant use.
英2 In order to recognize a symbol by its sign we must observe how it is used with a sense.
日 シンボルをその記号において認識するには、記号の有意義な使用に目をむけなければならない。
英1 The sign determines a logical form only together with its logical syntactic application.
英2 A sign does not determine a logical form unless it is taken together with its logico-syntactical employment.
日 論理的構文論にそった使用によってはじめて、記号の論理形式が定まる。
(Wenn sich alles so verhält als hätte ein Zeichen Bedeutung, dann hat es auch Bedeutung.)
英1 If a sign is not necessary then it is meaningless. That is the meaning of Occam's razor.
(If everything in the symbolism works as though a sign had meaning, then it has meaning.)
英2 If a sign is useless, it is meaningless. That is the point of Occam'smaxim. (If everything behaves as if a sign had meaning, then it does have meaning.)
日 使用されない記号は意味をもたない。これがオッカムの格言の意味である。
(もし、ある記号がすべての状況で意味をもつかのように見えるならば、その記号は意味をもっている。)
英1 In logical syntax the meaning of a sign ought never to play a role; it must admit of being established without mention being thereby made of the meaning of a sign; it ought to presuppose only the description of the expressions.
英2 In logical syntax the meaning of a sign should never play a role. It must be possible to establish logical syntax without mentioning the meaning of a sign: only the description of expressions may be presupposed.
日 論理的構文論において記号の意味はいかなる役割もはたしてはならない。論理的構文論は、記号の意味を問うことなしに築かれねばならない。それは、ただ表現を記述することのみを前提としなければならない。
英1 From this observation we get a further view -- into Russell's Theory of Types. Russell's error is shown by the fact that in drawing up his symbolic rules he has to speak about the things his signs mean.
英2 From this observation we turn to Russell's 'theory of types'. It can be seen that Russell must be wrong, because he had to mention the meaning of signs when establishing the rules for them.
日 この観点からラッセルの「タイプ理論」を見渡してみる。ラッセルの誤りは、記号の規則を立てるのに記号の意味を論じなければならなかったことに示されている。
英1 No proposition can say anything about itself, because the propositional sign cannot be contained in itself (that is the whole "theory of types").
英2 No proposition can make a statement about itself, because a propositional sign cannot be contained in itself (that is the whole of the'theory of types').
日 いかなる命題も自分自身について語ることはできない。なぜなら、ある命題記号が当の命題記号自身のうちに含まれることはないからである。(これが「タイプ理論」のすべてである。)
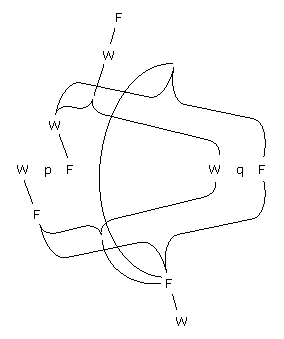
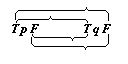
Nehmen wir nämlich an, die Funktion F(fx) könnte ihr eigenes Argument sein; dann gäbe es also einen Satz: »F(F(fx))« und in diesem müssen die äußere Funktion F und die innere Funktion F verschiedene Bedeutungen haben, denn die innere hat die Form φ(fx), die äußere die Form ψ(φ(fx)). Gemeinsam ist den beiden Funktionen nur der Buchstabe »F«, der aber allein nichts bezeichnet.
Dies wird sofort klar, wenn wir statt »F(Fu)« schreiben »(∃φ):F(φu).φu=Fu«.
Hiermit erledigt sich Russells Paradox.
英1 A function cannot be its own argument, because the functional sign already contains the prototype of its own argument and it cannot contain itself.
If, for example, we suppose that the function F(fx) could be its own argument, then there would be a proposition "F(F(fx))", and in this the outer functions F and the inner function F must have different meanings; for the inner has the form
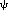 (fx), the outer the form
(fx), the outer the form 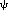 (
(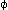 (fx)). Common to both functions is only the letter "F", which by itself signifies nothing.
(fx)). Common to both functions is only the letter "F", which by itself signifies nothing.This is at once clear, if instead of "F(F(u))" we write "(
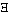
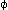 ) : F(
) : F(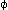 u) .
u) . 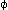 u=Fu".
u=Fu".Herewith Russell's paradox vanishes.
英2 The reason why a function cannot be its own argument is that the sign for a function already contains the prototype of its argument, and it cannot contain itself. For let us suppose that the function F(fx) could be its own argument: in that case there would be a proposition 'F(F(fx))', in which the outer function F and the inner function F must have different meanings, since the inner one has the form O(f(x)) and the outer one has the form Y(O(fx)). Only the letter 'F' is common to the two functions, but the letter by itself signifies nothing. This immediately becomes clear if instead of 'F(Fu)' we write '(do) : F(Ou) . Ou = Fu'. That disposes of Russell's paradox.
日 関数を自分自身の入力項とすることはできない。なぜなら、関数記号はすでに入力項のプロトタイプを含んでおり、そしてそのプロトタイプは自分自身を含むことができないからである。
例えば、関数
F(fx) が自分自身の入力項になりえると仮定してみよう。そのとき、「F(F(fx))」という命題が存在することになる。ところがこの命題において外側の関数 F と内側の関数 F は異なる意味をもっているのでなければならない。なぜならば、内側は φ(fx) という形式であるのに対し、外側は ψ(φ(fx)) となるからである。二つの関数に共通なものは文字「F」にすぎない。だが文字それ自身は何も表さない。このことは、「
F(Fu)」 の代わりに「(∃φ) : F(φu) . φu = Fu 」 と書くと、ただちに明らかになる。かくして、ラッセルのパラドックスは消え去る。
英1 The rules of logical syntax must follow of themselves, if we only know how every single sign signifies.
英2 The rules of logical syntax must go without saying, once we know how each individual sign signifies.
日 論理的構文論の規則は、個々の記号が表示する仕方を知りさえすれば、おのずから理解されるのでなければならない。
Zufällig sind die Züge, die von der besonderen Art der Hervorbringung des Satzzeichens herrühren. Wesentlich diejenigen, welche allein den Satz befähigen, seinen Sinn auszudrücken.
英1 A proposition possesses essential and accidental features.
Accidental are the features which are due to a particular way of producing the propositional sign. Essential are those which alone enable the proposition to express its sense.
英2 A proposition possesses essential and accidental features. Accidental features are those that result from the particular way in which the propositional sign is produced. Essential features are those without which the proposition could not express its sense.
日 命題は本質的な側面と偶発的な側面をもつ。
命題記号を生成する特定の方法に依存する側面は、偶発的である。
それなしには、命題がその意義を表現できない側面は、本質的である。
Und ebenso ist allgemein das Wesentliche am Symbol das, was alle Symbole, die denselben Zweck erfüllen können, gemeinsam haben.
英1 The essential in a proposition is therefore that which is common to all propositions which can express the same sense.
And in the same way in general the essential in a symbol is that which all symbols which can fulfil the same purpose have in common.
英2 So what is essential in a proposition is what all propositions that can express the same sense have in common. And similarly, in general, what is essential in a symbol is what all symbols that can serve the same purpose have in common.
日 それゆえ命題における本質的なものは、同じ意義を表現することのできるすべての命題が共有する。
同様に、シンボルにおいて本質的なものは、同じ目的を果たすことのできるすべてのシンボルが共有する。
英1 One could therefore say the real name is that which all symbols, which signify an object, have in common. It would then follow, step by step, that no sort of composition was essential for a name.
英2 So one could say that the real name of an object was what all symbols that signified it had in common. Thus, one by one, all kinds of composition would prove to be unessential to a name.
日 それゆえ本来の名とは、同じ対象を表示するシンボルすべてに共通するものである、と言うこともできるだろう。こうして、いかなる合成も名にとって本質的でないことが、順々に示されるだろう。
英1 In our notations there is indeed something arbitrary, but this is not arbitrary, namely that if we have determined anything arbitrarily, then something else must be the case. (This results from the essence of the notation.)
英2 Although there is something arbitrary in our notations, this much is not arbitrary--that when we have determined one thing arbitrarily, something else is necessarily the case. (This derives from the essence of notation.)
日 われわれの表記法にはたしかに恣意的なところがある。しかし、恣意的であれ、あることを決めたならば、他のことがらはそれに応じて定まらねばならない。このことは、けっして恣意的ではない。(これは表記法の本質によっている)
英1 A particular method of symbolizing may be unimportant, but it is always important that this is a possible method of symbolizing. And this happens as a rule in philosophy: The single thing proves over and over again to be unimportant, but the possibility of every single thing reveals something about the nature of the world.
英2 A particular mode of signifying may be unimportant but it is always important that it is a possible mode of signifying. And that is generally so in philosophy: again and again the individual case turns out to be unimportant, but the possibility of each individual case discloses something about the essence of the world.
日 特定の表示方法は重要でないとしても、その表示方法が可能であること、それは常に重要である。とくに哲学において重要である。個別例は重要ではないとたびたび指摘されるが、しかし、そうした個々の事例の可能性は、世界の本質のなんらかを開示するのである。
英1 Definitions are rules for the translation of one language into another. Every correct symbolism must be translatable into every other according to such rules. It is this which all have in common.
英2 Definitions are rules for translating from one language into another.Any correct sign-language must be translatable into any other in accordance with such rules: it is this that they all have in common.
日 定義とは、ある言語から他の言語への翻訳規則である。すべての正しい記号言語は、そのような規則によって任意の他の言語へ翻訳可能でなければならない。これが、すべての正しい記号言語が共有するものである。
英1 What signifies in the symbol is what is common to all those symbols by which it can be replaced according to the rules of logical syntax.
英2 What signifies in a symbol is what is common to all the symbols that the rules of logical syntax allow us to substitute for it.
日 シンボルにおいて表示するもの、それは、論理的構文論の規則によって、それと置換可能なすべてのシンボルが共有するものである。
(Hiermit ist die Art und Weise gekennzeichnet, wie eine spezielle mögliche Notation uns allgemeine Aufschlüsse geben kann.)
英1 We can, for example, express what is common to all notations for the truth-functions as follows: It is common to them that they all, for example, can be replaced by the notations of "~p" ("not p") and "p v q" ("p or q").
(Herewith is indicated the way in which a special possible notation can give us general information.)
英2 For instance, we can express what is common to all notations for truth-functions in the following way: they have in common that, for example, the notation that uses 'Pp' ('not p') and 'p C g' ('p or g') can be substituted for any of them. (This serves to characterize the way in which something general can be disclosed by the possibility of a specific notation.)
日 たとえば、真理関数*の表記すべてに共通なものは、次のように言い表せる。--どの真理関数の表記も、たとえば、「
~p」(「p ではない」)と「pVq」(「p または q」)という表記を用いて書き換えることができる。それはすべての真理関数の表記に共通である。(このように、特殊な表記であってもそれが可能であるということが、一般的な何ごとかを開示しうるのであり、この例はその方法を示している。)
英1 The sign of the complex is not arbitrarily resolved in the analysis, in such a way that its resolution would be different in every propositional structure.
英2 Nor does analysis resolve the sign for a complex in an arbitrary way, so that it would have a different resolution every time that it was incorporated in a different proposition.
日 複合的なものに対する記号を分析し、解決する仕方も恣意的ではない。すなわち、その記号の現れる命題構造が異なるごとに解決が異なるわけではない。
英1 The proposition determines a place in logical space: the existence of this logical place is guaranteed by the existence of the consituent parts alone, by the existence of the significant proposition.
英2 A proposition determines a place in logical space.
The existence of this logical place is guaranteed by the mere existence of the constituents--by the existence of the proposition with a sense.
日 命題は論理空間に一つの領域を定める。この論理的領域の存在は、ひとえにその構成要素の存在によって、すなわち有意義な命題の存在によって、保証されている。
英1 The propositional sign and the logical co-ordinates: that is the logical place.
英2 The propositional sign with logical co-ordinates--that is the logical place.
日 命題記号と論理的座標、これが論理的領域を形づくる。
英1 The geometrical and the logical place agree in that each is the possibility of an existence.
英2 In geometry and logic alike a place is a possibility: something can exist in it.
日 幾何学的領域と論理的領域は、どちらも存在の可能性であるという点で一致している。
(Sonst würden durch die Verneinung, die logische Summe, das logische Produkt, etc. immer neue Elemente - in Koordination - eingeführt.)
(Das logische Gerüst um das Bild herum bestimmt den logischen Raum. Der Satz durchgreift den ganzen logischen Raum.)
英1 Although a proposition may only determine one place in logical space, the whole logical space must already be given by it.
(Otherwise denial, the logical sum, the logical product, etc., would always introduce new elements -- in co-ordination.)
(The logical scaffolding round the picture determines the logical space. The proposition reaches through the whole logical space.)
英2 A proposition can determine only one place in logical space:nevertheless the whole of logical space must already be given by it.
(Otherwise negation, logical sum, logical product, etc., would introduce more and more new elements in co-ordination.)
(The logical scaffolding surrounding a picture determines logical space. The force of a proposition reaches through the whole of logical space.)
日 一つの命題は論理空間に一つの領域しか定めないが、にもかかわらず、この一つの領域によって論理空間全体がすでに与えられていなければならない。
(さもなければ、否定や論理和、論理関などによって、つねに新たな要素が--論理的座標の中に--導入されなければならないことになる。)
(像をとりまく論理的足場が論理空間を定める。命題は論理空間全体へ手を伸ばす。)
英1 The applied, thought, propositional sign, is the thought.
英2 A propositional sign, applied and thought out, is a thought.
日 適用された、思考された、命題記号が思考である。
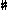 and
and 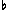 in the score).
in the score). 0 objects".
0 objects".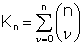 Möglichkeiten.
Möglichkeiten.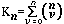 possibilities.
possibilities.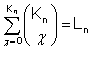 Möglichkeiten.
Möglichkeiten.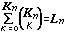 possibilities.
possibilities.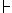 « ist logisch ganz bedeutungslos; er zeigt bei Frege (und Russell) nur an, dass diese Autoren die so bezeichneten Sätze für wahr halten. »
« ist logisch ganz bedeutungslos; er zeigt bei Frege (und Russell) nur an, dass diese Autoren die so bezeichneten Sätze für wahr halten. » " is logically altogether meaningless; in Frege (and Russell) it only shows that these authors hold as true the propositions marked in this way.
" is logically altogether meaningless; in Frege (and Russell) it only shows that these authors hold as true the propositions marked in this way.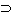 p . q
p . q  q]
q] , . . . .) to elementary propositions.
, . . . .) to elementary propositions. )". "
)". "
 ,
,  ' (
' (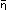 ) is therefore:
) is therefore: 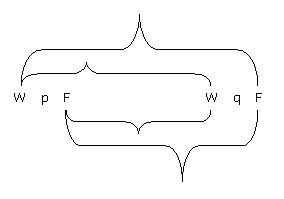
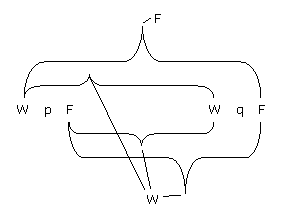

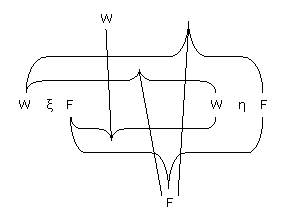
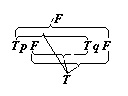
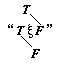
 " thus :--
" thus :--